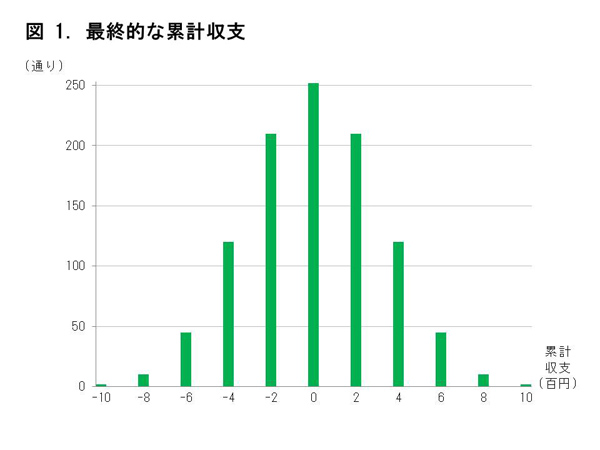
コイン投げゲームの累計収支は0を頂点とした山の形に(図1)
ギャンブルを楽しむためには、最終的な勝ち負けが大事だが、それだけではない。これまでのところ勝っているか、負けているかというゲームの途中経過も、楽しむための大きな要素となるはずだ。
最終的な累計収支の分布を見ると、直感的に、「勝っている状態(それまでの累計収支が、黒字の状態)と負けている状態(同じく、赤字の状態)は同じくらいあるのではないか」という感じがしてくる。この直感は正しいだろうか。
10回のコイン投げで、コインを1回投げるごとに、勝っている状態か、負けている状態かをみてみる。そして「黒字の状態の数-赤字の状態の数」として状態の差をとる。これを1024通りのそれぞれについて計算してみる。ただし、累計収支が0の状態は、黒字の状態や赤字の状態にはカウントしない。
10回とも裏で負けの場合は、当然累計収支は常に赤字なので状態の差は-10。6回裏が出た後に4回表が出た場合も、ずっと赤字のため状態の差は-10となる。
4回裏が出た後に6回表が出た場合は、8回目が終わったところで累計収支は0。それまでの7回は赤字、それ以降の2回は黒字なので、状態の差は-5となる。この場合は、最終的な累計収支は200円の黒字だが、負けている状態を多く味わっていたため途中経過を表す状態の差はマイナスとなるわけだ。
1024通りについて「黒字の状態の数-赤字の状態の数」の差をまとめると、図2のようになる。直感に反して、図の両端、つまりずっと黒字の状態である10や、ずっと赤字の状態である-10のケースが多い。
逆に、黒字と赤字の状態が同じになる、差が0のケースは一番少ない。つまり、「黒字と赤字のどちらかの状態ばかりを味わうことが多く、両方を同じくらいに経験することはあまりない」ということになる。
コインを投げる回数を10回よりも増やしていくと、黒字か赤字のどちらか極端な状態ばかりを味わうケースが増える。ケース数を表す棒グラフの結果を曲線でつないでみると、U字型になっていく(図の赤線)。この事象は「逆正弦法則(※注)」と呼ばれている。
※注/黒字と赤字の状態の差が一定範囲内にある確率を計算するには、この曲線の積分が必要となる。その際、逆正弦関数(サイン関数の逆関数)が現れるため、このような名前で呼ばれている。